Die Riemannsche Vermutung

Das Rätsel des Landes Riemannien

Irgendwo, weit hinter einer der unendlich vielen Dimensionen des Hilbert-Raums, befindet sich das Land Riemannien. Es wurde erst 1859 von Bernhard Riemann (1826-1866) entdeckt, daher trägt es seinen Namen. Riemann war Mathematiker, und auch die wenigen Pioniere, die bislang in dieses Land vorgedrungen sind, waren Mathematiker. Das wird wohl einige unter Ihnen abschrecken, lassen Sie mich dennoch einiges Wissenswerte über dieses Land erzählen.

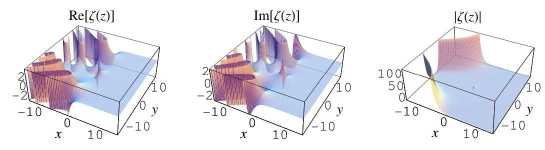
Das wohl Erstaunlichste an diesem Land ist, dass man von einer gleichen Landschaft zwei verschiedene Fotos schießen kann: Die Landschaft ist vierdimensional!

**Abbildung 1:** Drei Ansichten von Riemannien. Es sind die Graphen des Realteils $\mathrm{Re}\,\zeta(z)$ , des Imaginärteils $\mathrm{Im}\,\zeta(z)$ und des Absolutbetrags $\vert\zeta (z)\vert$ der Riemannschen Zeta-Funktion. ( $z = x + \mathrm{i}y \in\mathbb{C}$ .) Man erkennt die flache weite Ebene im Osten (x > 0), die Singularität bei s = 1, also x = 1 und y = 0, und die wilden Gebirge im Westen. Abb. von: http://mathworld.wolfram.com/RiemannZetaFunction.html

Die Mathematiker nennen die „Landschaft“ den Graphen der Riemannschen Zeta-Funktion, in Symbolen $\zeta(s)$ , wobei s eine so genannte komplexe Zahl ist. Komplexe Zahlen umfassen neben den reellen Zahlen die Quadratwurzeln negativer Zahlen, insbesondere die Zahl $\mathrm{i}= \sqrt{-1}$ . Sie lassen sich als Punkte der Ebene darstellen, wobei eine der zwei die Ebene aufspannenden Achsen die reellen Zahlen sind. Diese „reelle Achse“ ist die „Ost-West-Richtung“ unserer Landschaft, die Nord-Süd-Richtung wird aufgespannt von der „imaginären Achse“. Die Zeta-Funktion selber nimmt selber auch komplexe Werte an, und damit ist ihr Graph vierdimensional.

Da man auf einem Foto leider nur drei Dimensionen darstellen kann, greifen Mathematiker zu einem Trick und stellen den Graphen (wir erinnern uns: die „Landschaft“) in zwei Teilen dar, dem „Realteil“ und dem „Imaginärteil“. Um diese beiden Ansichten auf dieselbe Landschaft zu verbinden, betrachten manche Mathematiker den „Absolutbetrag“, das ist die Entfernung eines Landschaftspunkts vom Nullpunkt, dem „Ursprung“ der komplexen Ebene. Viele werden das als Länge des entsprechenden Vektors erkennen, und deren Quadrat ist nach dem Satz des Pythagoras gegeben als die Summe der Quadrate von Real- und Imaginärteil. Insgesamt ergibt damit das Foto des Absolutbetrags einen zwar etwas verzerrten, aber dennoch wichtigen Blick auf die Landschaft von Riemannien.

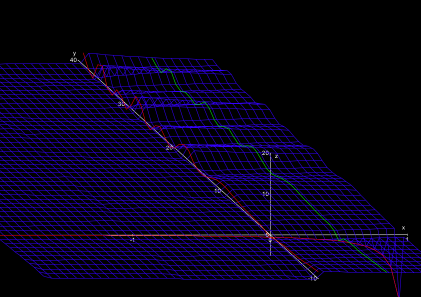
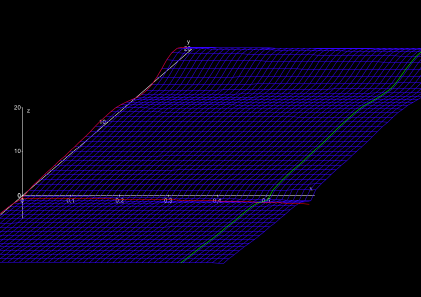
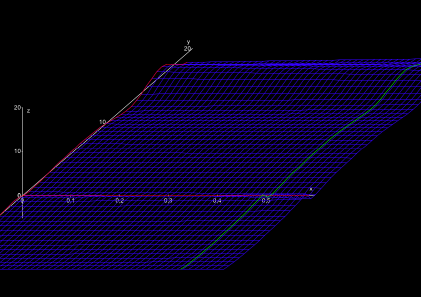
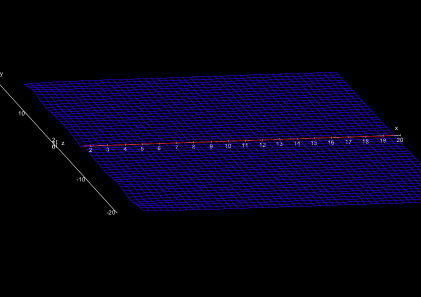
Setzt man die „Realbrille“ auf, so sieht man den Teil „Real-Riemannien“. Das ist eine eigenartige Landschaft. Im Osten erstreckt sich eine weite, ganz leicht abfallende Ebene (Abb. 2).

**Abbildung 2:** Die östliche Ebene 1 < Re s.
$\mathrm{Re}\,\zeta(s)$	$\mathrm{Im}\,\zeta(s)$	$\vert\zeta(s)\vert$

Nach Westen hin sieht man langsam ansteigende Hügelketten, die exakt in Ost-West-Richtung ausgerichtet sind.

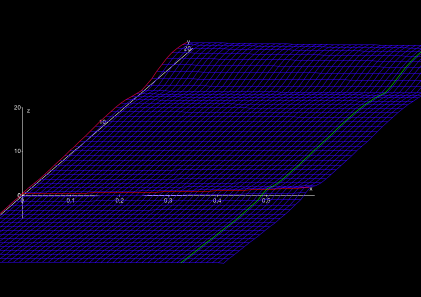
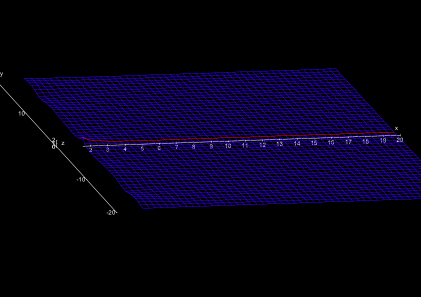
An einer speziellen Stelle (an der Koordinate s = 1) befindet sich ein unendlich hoher, steil aufschießender Berg, an den sich direkt ein unendlich tiefer Abgrund anschließt. Diese Stelle sollte man tunlichst vermeiden. Aber Riemann hatte bereits heraus gefunden, dass dies die einzige gefährliche ("singuläre") Stelle des Landes war (Abb. 3).

**Abbildung 3:** Die Umgebung der Singularität s = 1. Wie üblich sind die Graphen des Realteils $\mathrm{Re}\,\zeta(z)$ , des Imaginärteils $\mathrm{Im}\,\zeta(z)$ , und des Absolutbetrags $\vert\zeta (z)\vert$ der Riemannschen Zeta-Funktion dargestellt.
$\mathrm{Re}\,\zeta(s)$	$\mathrm{Im}\,\zeta(s)$	$\vert\zeta(s)\vert$

In der „Realansicht“ ist der Abgrund westlich des Berges, in der „Imaginäransicht“ ist er nördlich des Berges.

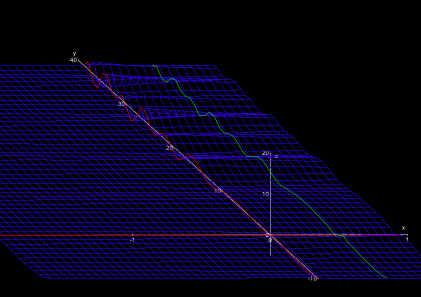
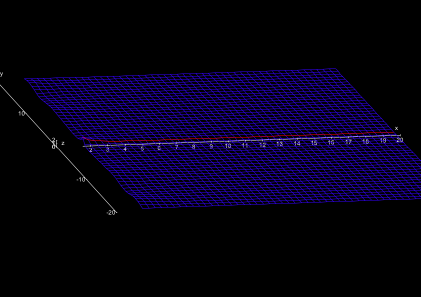
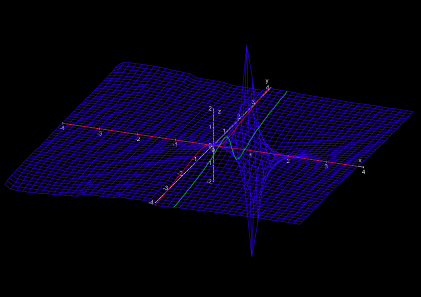
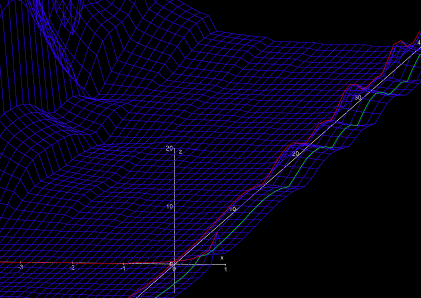
Ab dem nullten Längengrad in Süd-Nord-Richtung (der imaginären Achse s = iy) ändert sich der Charakter der Landschaft plötzlich. Die sanften Hügelketten brechen abrupt ab und münden in eine zunächst sehr ruhige, sanft gewellte Ebene (Abb. 4).

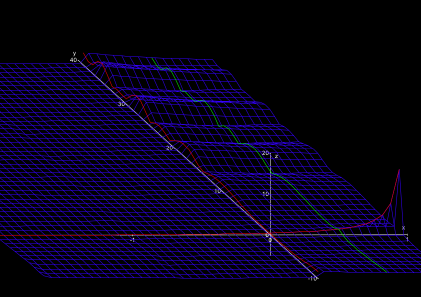
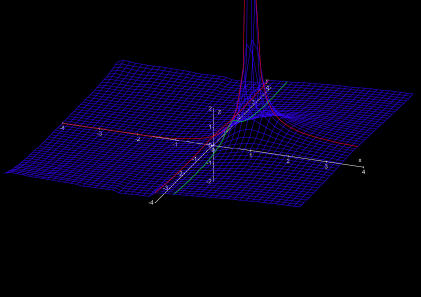
**Abbildung 4:** Der abrupte Landschaftswechsel an der imaginären Achse Re s = 0 (dem „nullten Längengrad“). Die rote Linie in Nord-Süd-Richtung ist die Projektion der Imaginärachse y auf den Graphen der Zeta-Funktion, die rote Linie in West-Ost-Richtung ist die Projektion der reellen Achse x.
$\mathrm{Re}\,\zeta(s)$	$\mathrm{Im}\,\zeta(s)$	$\vert\zeta(s)\vert$

Der friedliche Eindruck dieser neuen Landschaftsform trügt allerdings, im Nordwesten und Südwesten türmen sich gewaltige Gebirge mit steilen Gipfeln und zerklüfteten Abgründen (Abb. 5). Im Gegensatz zu der Singularität s = 1 jedoch sind die Berge und Abgründe nicht unendlich hoch bzw. tief, es sind keine Singularitäten. Sie umschließen ein nach Westen schnell enger werdendes Tal um den nullten Breitengrad (die „reelle Achse“ Im s = 0).

**Abbildung 5:** Der Beginn der gewaltigen Gebirgszüge im Nordwesten. Südlich des nullten Breitengrades erstreckt sich ein fast identisch ausehendes zerklüftetes Gebirge.
$\mathrm{Re}\,\zeta(s)$	$\mathrm{Im}\,\zeta(s)$	$\vert\zeta(s)\vert$

Das große Rätsel des Landes Riemannien

Das größte Rätsel der Landschaft von Riemannien ist die Verteilung der der „Nullstellen“. Damit meinen die Mathematiker diejenigen Orte, die sich gleichzeitig im Real- als auch im Imaginärteil genau auf Höhe Normalnull (NN) befinden. Bei weitem die meisten Stellen Riemanniens sind nicht NN. So ist die gesamte Ebene östlich der Singularität s = 1 über NN, und auch die zerklüfteten Gebirge im Westen sind nie gleichzeitig im Real- und Imaginärteil NN. Allein auf zwei Geraden kennt man solche Nullstellen, der reellen Achse und der „kritischen Geraden“. Auf der reellen Achse Im s = 0, also dem nullten Breitengrad, sind genau alle negativen geraden Werte von s Nullstellen,

s = -2, -4, -6, ...

Das sind die so genannten trivialen Nullstellen“. Die kritische Gerade dagegen ist eine Parallele der imaginären Achse (ein „Längengrad“ in Süd-Nord-Richtung), nämlich alle Zahlen mit Realteil $\frac12$ , d.h. $\mathrm{Re}\,s = \frac12$ . In den Abbildungen ist die kritische Linie grün eingezeichnet.

Man weiß heute nur, dass alle nichttrivialen Nullstellen auf dem „kritischen Streifen“ zwischen den Längengraden 0 und 1 (also 0 < Re s < 1), dass es auf der kritischen Geraden unendlich viele Nullstellen gibt, und dass mindestens 40% aller Nullstellen auf der kritischen Geraden liegen.

**Abbildung 6:** Der kritische Streifen 0 < Re s < 1. Die rote Linie in Nord-Süd-Richtung ist die Projektion der Imaginärachse y auf den Graphen der Zeta-Funktion, die rote Linie in West-Ost-Richtung ist die Projektion der reellen Achse x. Die kritische Linie $\mathrm{Re}\,s = \frac12$ ist grün.
$\mathrm{Re}\,\zeta(s)$	$\mathrm{Im}\,\zeta(s)$	$\vert\zeta(s)\vert$

Doch niemand weiß bis heute, ob wirklich alle nichttrivialen Nullstellen auf der kritischen Geraden liegen. Das ist die Riemann'sche Vermutung. Dieses Rätsel ist den Mathematikern so wichtig, dass es für denjenigen, der streng beweisen kann, dass alle nichttrivialen Nullstellen der Zeta-Funktion auf der kritischen Geraden liegen, eine Belohnung von 1 Million $ gibt! Eigenartigerweise gibt es wohl keine Belohnung, wenn die Vermutung falsch ist und jemand mindestens ein Gegenbeispiel findet: Sollte also jemand eine nichttriviale Nullstelle finden, die nicht auf der kritischen Geraden liegt, so ist das Rätsel zwar gelöst, aber es gibt keine Belohnung ....

Ein Programm zur Erkundung Riemannien

Wenn Sie das Land Riemannien auf eigene Faust erkunden wollen, so können Sie ein kleines Java-Programm herunterladen und eine Animation starten, die die Landschaft (zumindest für relativ kleine Werte von s) zeigt. Der Link dazu:

http://math-it.org/Mathematik/Riemann/riemann.jar

(Erfordert Java JRE 6 oder höher.)

Sie können dort die Bereiche der Variablenwerte Re s, Im s und z festlegen, in denen der Graph gezeigt werden soll. Hierbei ist s = Re s + i Im s, und jeweils z = Re ζ(s), z = Im ζ(s) bzw. z = |ζ(s)|.

In der Darstellung diese Programms sind die reelle und die imaginäre Achse jeweils als rote Linien auf den Graphen projiziert. Die sogenannte „kritische Gerade“ (Re s = 1/2) ist grün markiert; die berühmte Riemannsche Vermutung besagt, dass alle Nullstellen neben s = -2, -4, -6, .... auf der kritischen Gerade liegen.

Falls für Ihren Browser Java installiert ist und Sie die Ausführung dieses Applets erlauben, können Sie das Programm durch Anklicken der dann erscheinenden Schaltfläche starten:

Literatur und Quellen

Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. Verlag C.H. Beck, München 2004
http://www.maths.tcd.ie/pub/HistMath/People/Riemann/ – Biographie und Originalarbeiten von Bernhard Riemann
http://www.claymath.org/millennium-problems/riemann-hypothesis – Die Riemannsche Vermutung als eines der Milleniumsprobleme des Clay Mathematics Institute, für deren Lösung es jeweils 1 Million US-Dollar Belohnung gibt.