Shadows of Rotating Black Holes
 deutsch

Although a black hole is not visible, you can observe it nonetheless - it casts a shadow if it is in front of a bright background. Since the early 1970's (Bardeen 1973, Luminet 1979, Quien et al. 1995, Hollywood and Melia 1997, Falcke et al. 2000, Bromley et al. 2001) the apparent shapes of special black holes have been computed, de Vries (2000) plotted the shadows of general rotating and electrically charged black holes, in dependence on their angular momentum and charge. You can press the following button to let such shadow curves be drawn.

Please download the Java plugin at java.sun.com/products/plugin/

In the sequel you will find concise explanations about: How can these shadow curves be determined? What are the basic principles of the computations?

Geometrical optics

The key idea to compute the apparent shape of a general black hole relies on geometrical optics: an electromagnetic wave propagates approximately on a congruence of light rays perpendicular to the wave fronts. Now, according to general relativity, light rays are bended lines in a space-time curved by existing masses.

However, the geometric optics approximation is valid only if the wavelength λ is small as compared to the typical radius of curvature in the considered space-time region. For a black hole of solar mass, e.g., the so-called event radius r+ (the "rim" of the black hole) is about 1.5 km, that is the same magnitude as the radius of curvature close to it. Therefore, for medium wave radiation (with λ between 100 m and 1 km) originated close to its event horizon geometrical optics is not an admissible approximation, but for very high frequency it is, a fortiori for even shorter waves like infrared waves, light, or x-rays.

For the center of our Milky Way, presumably a giant black hole of about 2.6 million solar masses, the radius of curvature is about 4 million km, i.e., the error of a measurement of a long wave source (λ about 10 km) close to the event horizon is about 1:400000.

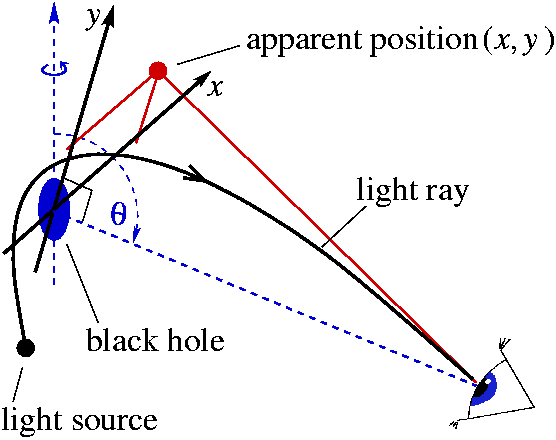
If we put up with inaccuracy of geometric optics, we get aware of the world around us as an optical illusion. Since the light rays reaching an observer in infinity are curved, they appear to come from a totally different direction. To represent the apparent source location with respect to the projection plane of the observer the (x, y) coordinates are used, as explained in the following figure:

ray illusion
Fig. 1. The (x,y) coordinates, indicating the apparent position of a light ray with respect to the observer's projection plane containing the center of the space-time: x denotes the apparent distance from the rotation axis, and y the projection of the rotation axis itself (dashed line). theta denotes the angle of latitude (reaching from the north pole at theta = 0 to the south pole at theta = pi).

Closed photon orbits

Further analysis of the light rays in a general Kerr-Newman space-time (a generalization of a rotating, electrically charged black hole) with a singularity shows the existence of photons which move on closed orbits (Bardeen 1973, Chandrasekhar 1983, de Vries 2000), i.e., on ellipses. Such orbits describe the limit of the innermost photon orbits coming from infinity and escaping back to infinity. (Here "infinity" means the asymptotically flat space-time region far away from the black hole; yet already at a distance of 25 times the event radius, 25r+, the radius of curvature is R = 125r+, so the asymptotically flat regions are reached rather quickly.)

Thus for an observer at infinity, who sees the black hole in front of an illuminated background in the asymptotic flat region, the black hole casts a shadow which in the approximation of geometrical optics is given by the set of its closed photon orbits.

de Vries (2000) has analyzed the nonlinear system of differential equations governing closed photon orbits. He found that for a Kerr-Newman space-time (that is a space-time generalization of a black hole) with mass M angular momentum a and electrical charge Q, the apparent position of a photon moving on a closed orbit with radius r in the (x, y) reference frame of an asymptotic observer located in the angle of latitude theta is given by

x = rD + rQ2 - M (r2 - a2)
a (r-M) sin theta

y2 = 4r2D - ( x - a sin theta)2.
(r-M)2

with D = r2 - 2Mr + a2 + Q2. For parameters satisfying the "cosmic censorship hypothesis" (Penrose 1979), prohibiting naked singularities, viz. M2 ≤ a2 + Q2 (de Vries and Schmidt-Kaler 2002), these formulas yield well-defined closed curves on the celestial sphere of the asymptotic observer, the black hole shadow curves. Please click the following button to let some shadow curves be drawn.

Please download the Java plugin at java.sun.com/products/plugin/

If you only see a gray area instead of a clickable button directly above this line, the probable reason is that you have not installed the newest Java plug-In. The applet is based upon the Java 2 classes (Swing), so to use it your browser needs the Java plug-in version 1.3 or higher. You can download it for free from the SUN website:

http://java.sun.com/getjava/download.html
or
http://java.sun.com/products/plugin/

References


Further links:

© de Vries 2003 federstrich Home